Modular Manifolds

Llama-Factory, Qwen3-Omni

ThinkingMachines wrote a rather interesting and in depth piece on the Modular Manifolds.

The fundamental challenge in training large neural networks lies in maintaining tensor health—ensuring that weights, activations, and gradients neither grow excessively large nor become vanishingly small. Traditional approaches have focused extensively on normalizing activations through techniques like layer normalization and gradient normalization through optimizers like Muon, but weight matrix normalization remains under-explored despite its potential benefits for training stability and predictability.

This post specifically presents a framework “modular manifolds” that constrains weight matrices to specific geometric structures (manifolds) while co-designing optimization algorithms that respect these constraints. This approach promises several advantages:

1. simplified hyperparameter tuning by focusing on tensors whose size matters most,

2. prevention of weight norm explosions,

3. improved matrix conditioning for more predictable behavior

4. facilitation of Lipschitz guarantees for robustness.

Before explaining further, let’s look at some basic concepts especially what Manifold is.

Manifold Concepts

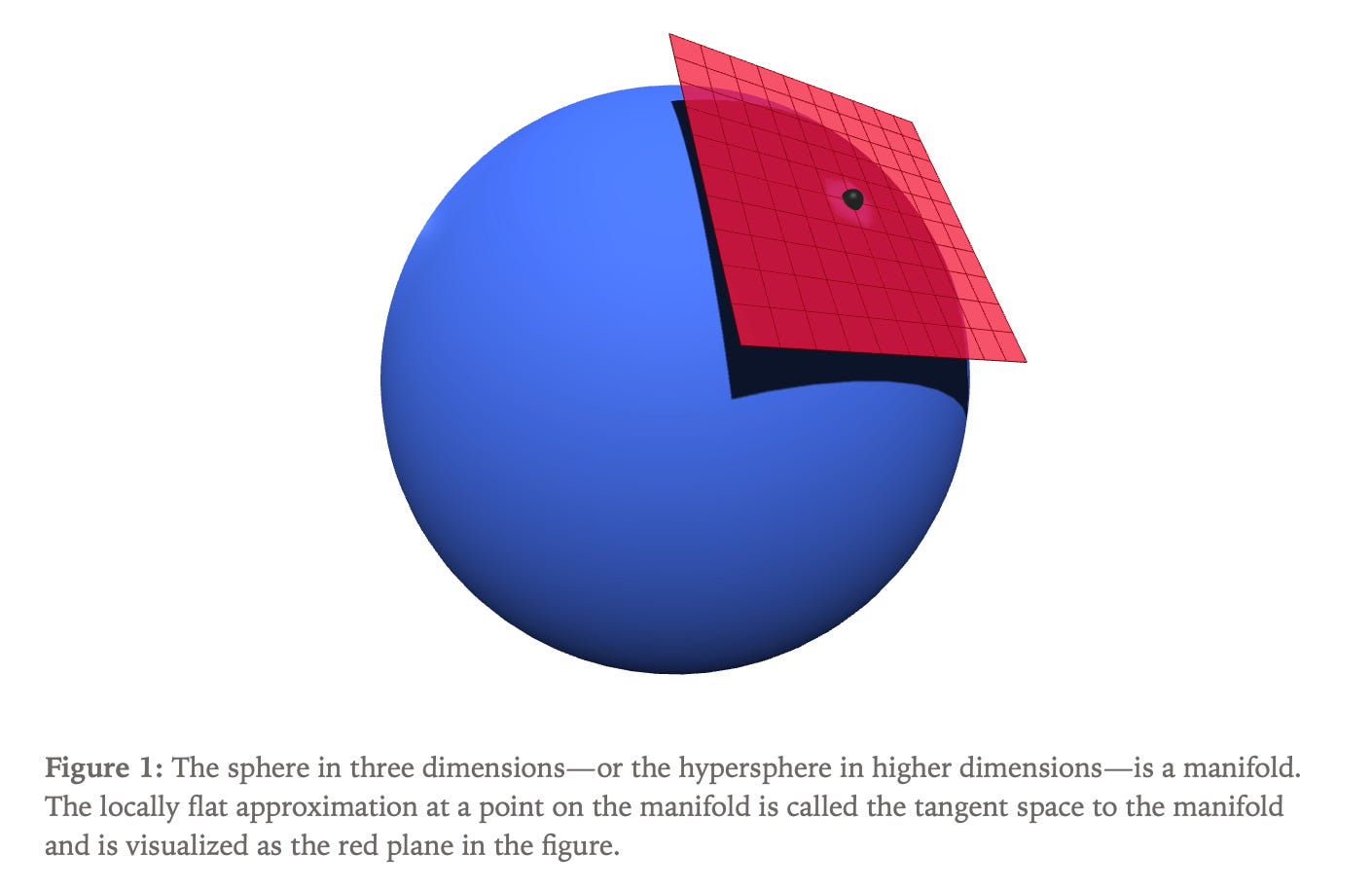
A manifold represents a curved surface that appears locally flat when examined closely, with the locally flat approximation at any point called the tangent space. The key insight is that optimization should occur within the tangent space rather than projecting updates back onto the manifold after each step, ensuring that the learning rate corresponds directly to the actual optimization step length.

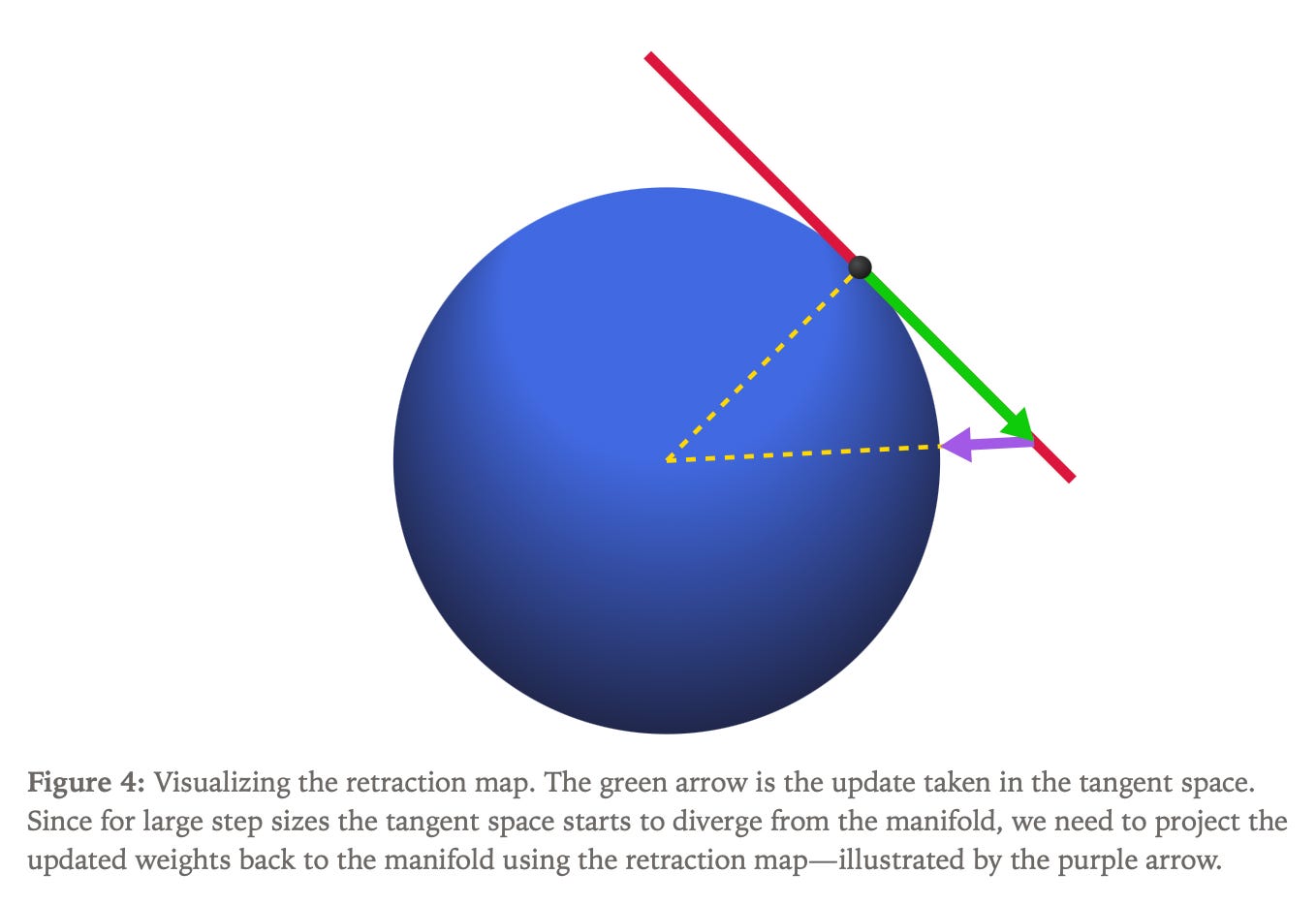
The fundamental principle involves three sequential steps for any manifold optimizer:

• finding the unit-length tangent vector that maximizes progress in the gradient direction,

• scaling this direction by the learning rate and updating weights

• retracting the updated weights back onto the manifold.

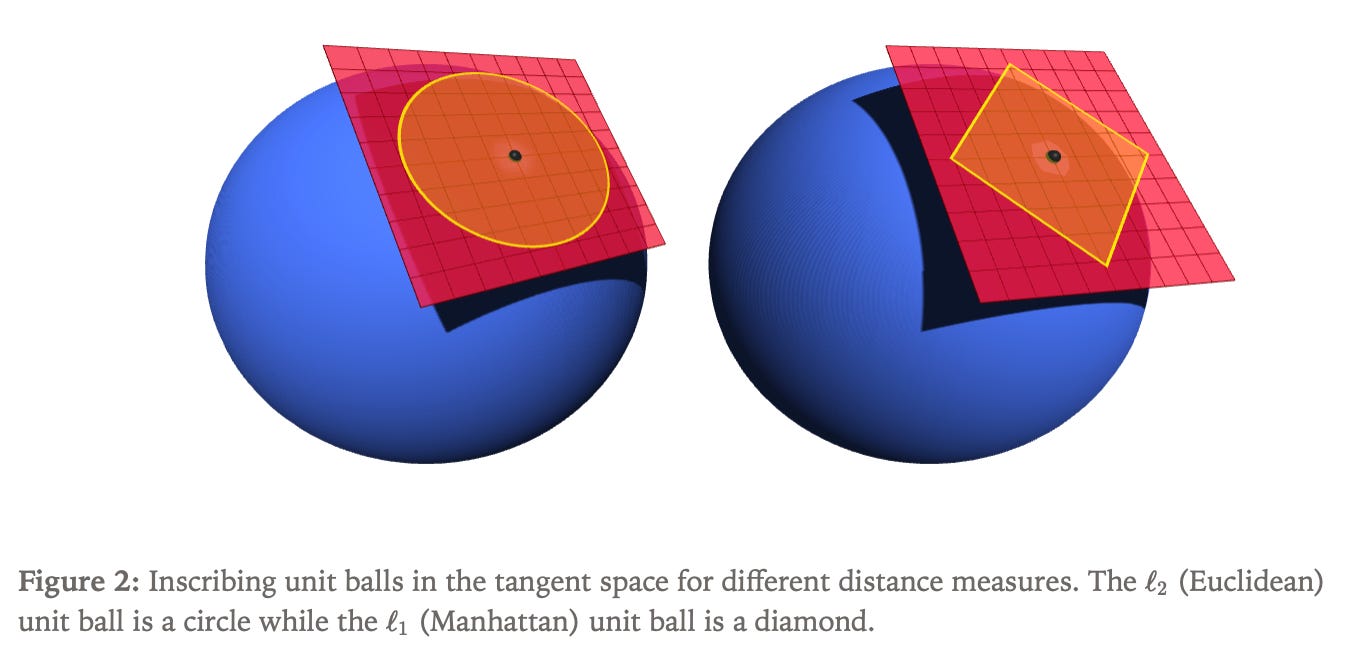
The choice of distance measurement in the tangent space critically affects the optimal update direction, with non-Euclidean distance measures potentially enabling greater progress toward the gradient direction for fixed step length.

The optimization problem considers constraining a vector parameter to a hypersphere in d-dimensional space, where all points maintain unit Euclidean norm. The tangent space at any point consists of vectors orthogonal to the current position, and the problem turns into a constrained minimization seeking the update direction that minimizes linear change in loss while satisfying both size and tangent constraints.

Using Lagrange multipliers, the optimal update formula emerges as subtracting the radial component from the gradient, normalizing the result, and multiplying by the learning rate. The retraction map, derived through Pythagoras’ theorem, involves dividing updated weights by the square root of one plus the squared learning rate to maintain the spherical constraint.

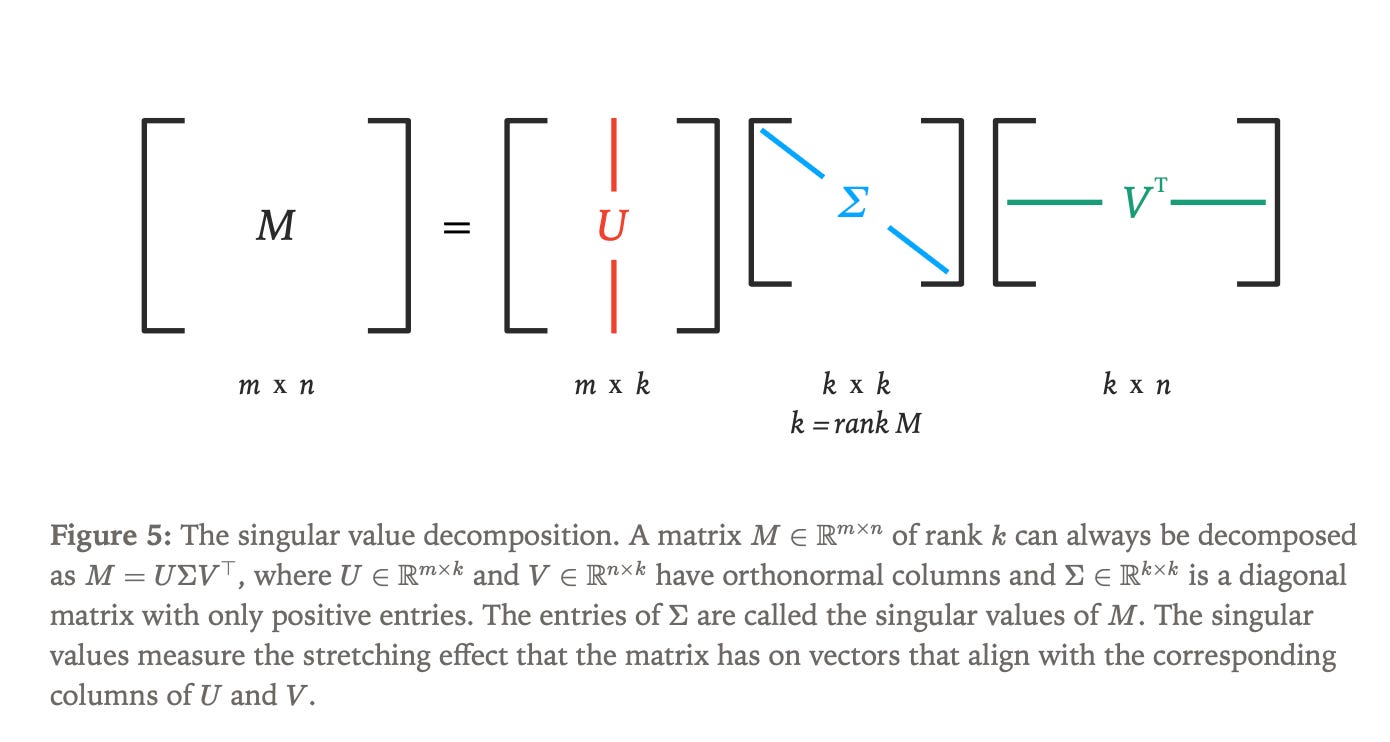
Extending manifold optimization to matrix parameters requires careful consideration of how weight matrices function within neural networks. Most transformer weight matrices act as “vector-multipliers,” transforming input vectors through matrix multiplication, and their behavior can be understood through singular value decomposition, which reveals how matrices stretch input vectors along different axes.

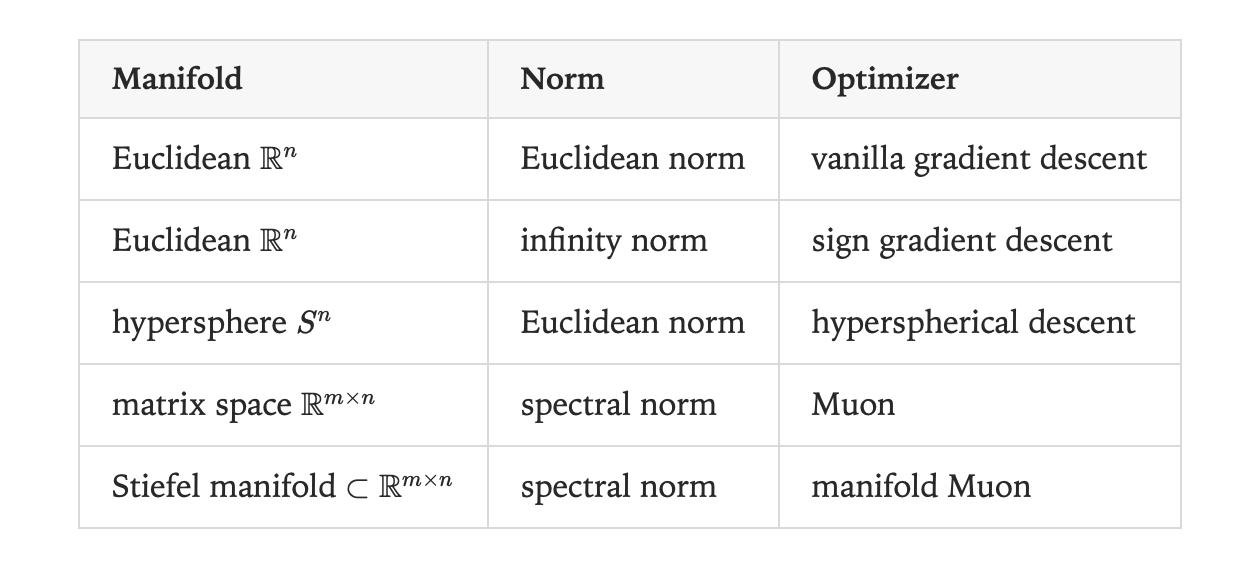
The Stiefel manifold becomes as the natural choice for matrix constraints, defined as the set of matrices where all singular values equal one, ensuring that the matrix neither excessively amplifies nor diminishes input vectors. For tall matrices (m ≥ n), this manifold can be characterized by the constraint W^T W = I_n, directly generalizing the hyperspherical constraint from vector parameters.

The manifold Muon algorithm combines Stiefel manifold constraints with spectral norm distance measurement to limit the maximum stretching effect of weight updates. This formulation leads to a constrained optimization problem that can be solved through dual ascent methodology, converting the original constrained minimization into an unconstrained maximization problem.

The solution involves introducing Lagrange multipliers and applying a series of mathematical transformations, ultimately yielding a dual problem solvable by gradient ascent. The complete algorithm consists of four steps: running gradient ascent on dual variables to find optimal Lagrange multipliers, computing the optimal update using the matrix sign function applied to a combination of gradients and weighted matrices, applying this update to the weights, and retracting weights back to the manifold using the matrix sign function.

The manifold Muon problem generalizes the hyperspherical case to matrices, seeking update directions that minimize gradient alignment subject to spectral norm constraints and tangent space requirements. The matrix sign function, which normalizes singular values to one, plays a central role in both computing optimal updates and performing manifold retraction.

The dual ascent approach transforms the problem through multiple steps:

• reformulating as a saddle point problem where maximization over Lagrange multipliers penalizes tangent space violations,

• applying trace properties and Sion’s minimax theorem,

• solving the inner minimization to obtain optimal updates parameterized by Lagrange multipliers,

• deriving the dual function involving nuclear norm gradients

The modular manifolds framework addresses the crucial question of how manifold constraints interact when combining layers to build complete networks. Rather than requiring global coordination, the theory enables reasoning about individual layers in isolation while automatically handling inter-layer interactions through a principled abstraction.

Any neural network module is characterized by three mathematical attributes: a forward function mapping from parameter space and input space to output space, a submanifold constraining the weights, and a norm serving as a measuring stick on weight space. For example, a Stiefel-constrained linear module combines linear transformation with Stiefel manifold constraints and spectral norm measurement.

When composing two modules, specific rules ensure that Lipschitz properties are preserved and automatically compiled for the joint system. The new forward function results from composing existing forward functions, the new manifold constraint becomes the Cartesian product of existing manifolds, and the new norm function represents the maximum of existing norm functions weighted by special scalar coefficients.

These scalar coefficients serve as learning rate budgets across layers, emerging naturally from the mathematical structure rather than requiring manual tuning. The composite norm automatically derives separate optimizers for each layer while the coefficients handle learning rate allocation, ensuring that updates respect the overall network’s Lipschitz properties.

Lipschitz Analysis

Budgeting learning rates across layers directly relates to understanding network output sensitivity with respect to weights. Manifold constraints enable much tighter bounds on this sensitivity compared to unconstrained approaches. For instance, a Stiefel-constrained linear module with unit-norm inputs maintains Lipschitz properties with constant one, meaning output changes are bounded by weight perturbation magnitude measured in spectral norm. This Lipschitz statement extends automatically to composed modules following the composition rules, providing principled foundations for scaling weight updates throughout the network. Practical implementation of manifold optimization requires efficient computation of several mathematical operations, particularly the matrix sign function used in manifold Muon. Recent research like the Polar Express algorithm show promise for fast matrix sign computation on GPUs, but further algorithmic innovations may be necessary for large-scale deployment.

The dual ascent approach in manifold Muon involves iterative optimization to solve for Lagrange multipliers, potentially requiring multiple inner iterations per optimization step. This computational overhead must be weighed against benefits of improved conditioning and stability, particularly for large models where training stability is paramount.

Modularity and Architecture Design

The modular manifolds framework opens numerous questions about optimal manifold choices for different network components. Attention heads and embeddings may benefit from different constraint types, and the framework naturally accommodates mixed constraint patterns where some tensors remain unconstrained.

Architecture-optimizer co-design represents a promising direction, where manifold constraints exemplify tight integration between architectural components and optimization algorithms. While hard manifold constraints may not ultimately prove optimal, they demonstrate the potential for discovering new co-design opportunities.

Advanced Optimization Techniques

The dual ascent formulation of manifold Muon suggests opportunities for applying more sophisticated convex optimization techniques to solve dual problems faster and more reliably. Convergence analysis remains an open question, particularly regarding whether improved weight matrix conditioning accelerates overall convergence.

Regularization effects of manifold constraints deserve deeper investigation, including whether constraint radii can be tuned to improve generalization performance. The implicit regularization provided by manifold constraints may offer new approaches to controlling model complexity.

Most manifold optimization research operates within Riemannian geometry where distances derive from inner products. However, neural networks naturally involve operator norms like the spectral norm that do not emerge from inner products, creating non-Riemannian geometric structures with sharp-cornered norm balls and non-unique gradient flows.

This non-Riemannian world may harbor undiscovered optimization principles particularly relevant to neural network training. The geometric structure of neural network weight spaces may provide insights into more effective optimization approaches.

Challenges

Scaling manifold optimization techniques to contemporary large models requires addressing several practical considerations. Efficient GPU implementations of manifold operations remain crucial, particularly for operations like matrix sign computation that may not have optimized implementations in standard deep learning frameworks. Memory overhead associated with storing dual variables and performing additional computations must be balanced against training benefits.

Connection to Existing Optimization Theory

This framework provides a principled approach to understanding how local optimization decisions affect global network behavior through compositional Lipschitz analysis.

The relationship between manifold constraints and existing regularization techniques deserves further exploration, particularly understanding how geometric constraints relate to more familiar penalty-based approaches. The automatic learning rate budgeting emerging from modular manifold composition offers an alternative to manual hyperparameter tuning that may prove more principled and effective.

Impact on Training

By constraining weight matrices to well-conditioned manifolds, the approach may fundamentally alter training dynamics in ways that improve both stability and convergence. The elimination of weight norm explosions and the guarantee of bounded condition numbers create more predictable training behavior that may be particularly valuable for large-scale experiments.

The Lipschitz guarantees provided by manifold constraints offer robustness benefits that extend beyond optimization to model deployment, where bounded sensitivity to input perturbations provides security and reliability advantages.

Libraries

Llama-Factory is a library that provides Unified Efficient Fine-Tuning of 100+ LLMs & VLMs (ACL 2024).

Features

• Various models: LLaMA, LLaVA, Mistral, Mixtral-MoE, Qwen, Qwen2-VL, DeepSeek, Yi, Gemma, ChatGLM, Phi, etc.

• Integrated methods: (Continuous) pre-training, (multimodal) supervised fine-tuning, reward modeling, PPO, DPO, KTO, ORPO, etc.

• Scalable resources: 16-bit full-tuning, freeze-tuning, LoRA and 2/3/4/5/6/8-bit QLoRA via AQLM/AWQ/GPTQ/LLM.int8/HQQ/EETQ.

• Advanced algorithms: GaLore, BAdam, APOLLO, Adam-mini, Muon, OFT, DoRA, LongLoRA, LLaMA Pro, Mixture-of-Depths, LoRA+, LoftQ and PiSSA.

• Practical tricks: FlashAttention-2, Unsloth, Liger Kernel, RoPE scaling, NEFTune and rsLoRA.

• Wide tasks: Multi-turn dialogue, tool using, image understanding, visual grounding, video recognition, audio understanding, etc.

• Experiment monitors: LlamaBoard, TensorBoard, Wandb, MLflow, SwanLab, etc.

• Faster inference: OpenAI-style API, Gradio UI and CLI with vLLM worker or SGLang worker.

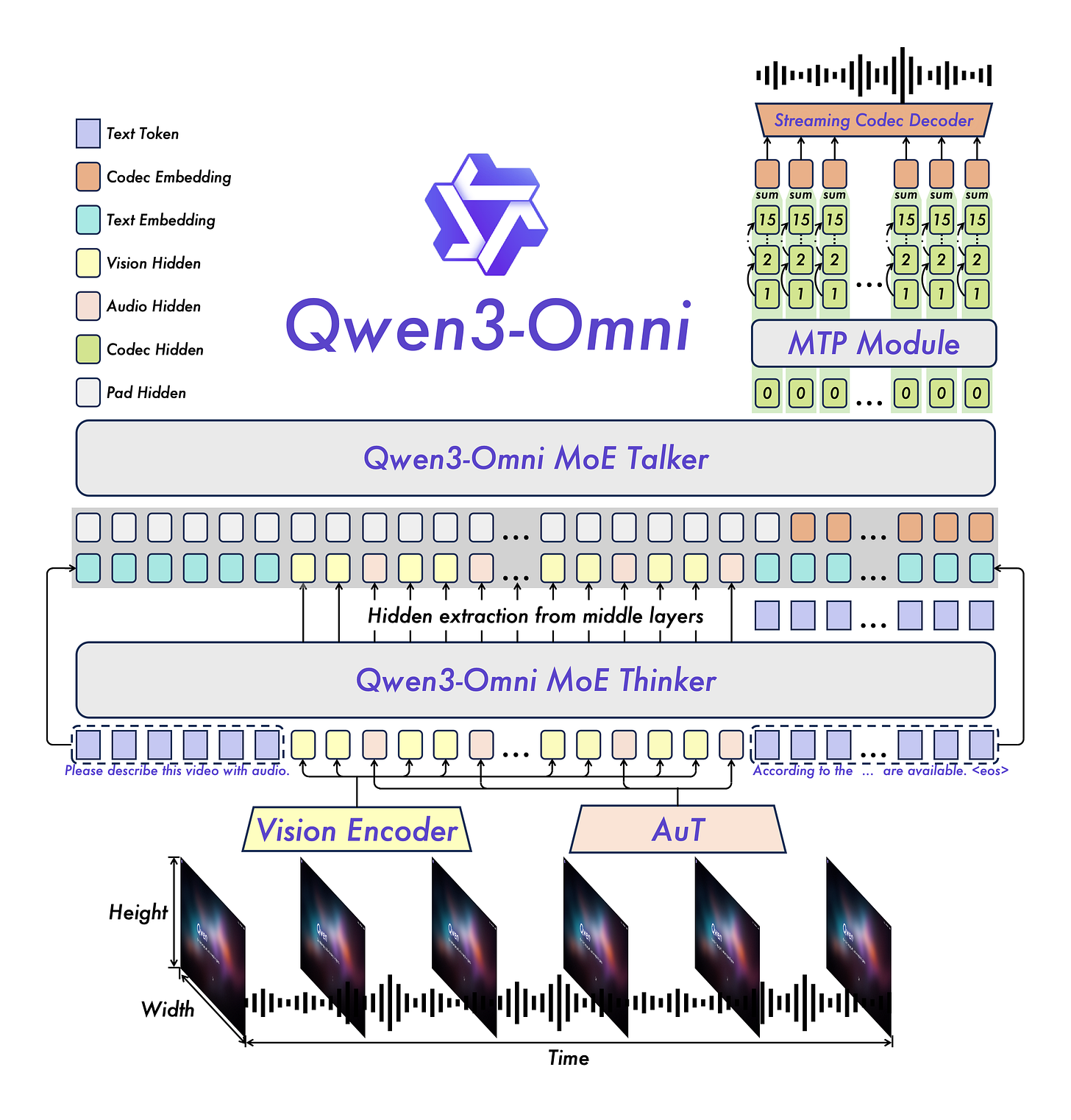
Qwen3-Omni is the natively end-to-end multilingual omni-modal foundation models. It processes text, images, audio, and video, and delivers real-time streaming responses in both text and natural speech. We introduce several architectural upgrades to improve performance and efficiency.

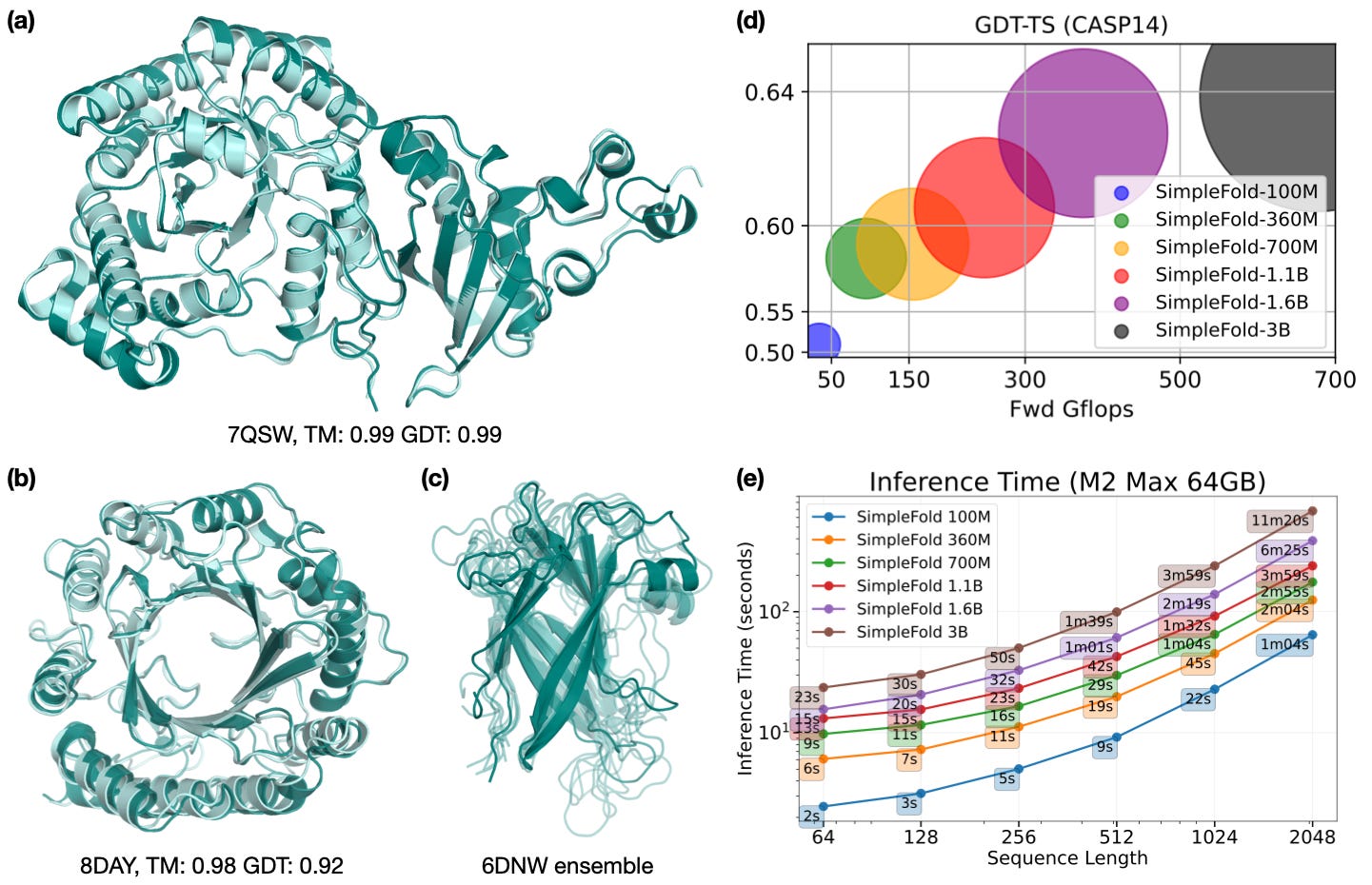
SimpleFold, the first flow-matching based protein folding model that solely uses general purpose transformer layers. SimpleFold does not rely on expensive modules like triangle attention or pair representation biases, and is trained via a generative flow-matching objective. SimpleFold can scale to 3B parameters and train it on more than 8.6M distilled protein structures together with experimental PDB data. To the best of researchers’per knowledge, SimpleFold is the largest scale folding model ever developed. On standard folding benchmarks, SimpleFold-3B model achieves competitive performance compared to state-of-the-art baselines. Due to its generative training objective, SimpleFold also demonstrates strong performance in ensemble prediction. SimpleFold challenges the reliance on complex domain-specific architectures designs in folding, highlighting an alternative yet important avenue of progress in protein structure prediction.

Claude Code Router allows you to use Claude Code as the foundation for coding infrastructure, and you can decide how to interact with the model while enjoying updates from Anthropic.

spaCy is a library for advanced Natural Language Processing in Python and Cython. It’s built on the very latest research, and was designed from day one to be used in real products.

• spaCy comes with pretrained pipelines and currently supports tokenization and training for 70+ languages. It features state-of-the-art speed and neural network models for tagging, parsing, named entity recognition, text classification and more, multi-task learning with pretrained transformers like BERT, as well as a production-ready training system and easy model packaging, deployment and workflow management.

Features

• Model Routing: Route requests to different models based on your needs (e.g., background tasks, thinking, long context).

• Multi-Provider Support: Supports various model providers like OpenRouter, DeepSeek, Ollama, Gemini, Volcengine, and SiliconFlow.

• Request/Response Transformation: Customize requests and responses for different providers using transformers.

• Dynamic Model Switching: Switch models on-the-fly within Claude Code using the /model command.

Below the Fold

zoxide is a smarter cd command, inspired by z and autojump.

It remembers which directories you use most frequently, so you can “jump” to them in just a few keystrokes.
zoxide works on all major shells.

• GitHub Actions Integration: Trigger Claude Code tasks in your GitHub workflows.

• Plugin System: Extend functionality with custom transformers.

SSH3 is a complete revisit of the SSH protocol, mapping its semantics on top of the HTTP mechanisms. It comes from our research work and we (researchers) recently proposed it as an Internet-Draft (draft-michel-remote-terminal-http3-00).

In a nutshell, SSH3 uses QUIC+TLS1.3 for secure channel establishment and the HTTP Authorization mechanisms for user authentication. Among others, SSH3 allows the following improvements:

• Significantly faster session establishment

• New HTTP authentication methods such as OAuth 2.0 and OpenID Connect in addition to classical SSH authentication

• Robustness to port scanning attacks: your SSH3 server can be made invisible to other Internet users

• UDP port forwarding in addition to classical TCP port forwarding

• All the features allowed by the modern QUIC protocol: including connection migration (soon) and multipath connections

SWE-Bench Pro is a challenging benchmark evaluating LLMs/Agents on long-horizon software engineering tasks. Given a codebase and an issue, a language model is tasked with generating a patch that resolves the described problem.