Linear Attention Mechanism Comparisons

More attention comparisons!

After seminal paper, Attention is all you need, all kinds of different derivative ideas are tried out to improve the original attention mechanism proposed in the paper. And people came up with a lot of good variations where the computational expensiveness of the original attention mechanism improved, more expressivity and some of the interesting properties like forgetting is incorporated into the original attention mechanism. For these different attention mechanisms, there was a lack of comparison in mathematical formula for different attention mechanisms and comparison in different dimensions of these derivative attention mechanisms.

Franz Louis Cesista provides a comprehensive analysis of linear attention mechanisms through the lens of blocked matrix formulation. He presents a mathematical framework for understanding these mechanisms, which are becoming increasingly important in efficient sequence modeling. Linear attention mechanisms offer computational advantages over traditional attention while maintaining modeling power, and this article explores their mathematical foundations, varieties, and implementation strategies.

Understanding Linear Attention Mechanisms

Core Concepts and Formulation

Linear attention mechanisms represent a family of efficient sequence models that typically follow a recursive update rule in the form of:

\(S_i = S_{i-1}A_i + B_i\)

S_{i-1} represents the state after processing the first i-1 tokens, S_i is the updated state after processing the first i tokens, and A_i and B_i are update matrices. The A_i matrix typically modifies information already stored in the state, while B_i adds new information. When

\(A_i \neq I\)

it generally removes some old information from the state, though it can also "invert" information if it has negative eigenvalues.

Key Variants of Linear Attention

The blog post discusses several prominent linear attention mechanisms, each with distinct characteristics:

Failed to render LaTeX expression — no expression found

Here, k_i and v_i represent the key-value pair for the i-th token, \alpha_i functions as a data-dependent weight decay, and \beta_i acts as a data-dependent learning rate.

Blocked Matrix Formulation

Mathematical Representation

The author introduces a more intuitive representation of linear attention mechanisms using blocked matrices. The update rule can be rewritten as:

\(\begin{bmatrix} S_{i} & I \end{bmatrix} = \begin{bmatrix} S_{i-1} & I \end{bmatrix} \begin{bmatrix} A_i & 0 \\ B_i & I \end{bmatrix}\)

This formulation provides clarity on how these mechanisms operate and can be computed efficiently. By unrolling this recurrence, we can derive a formula for the state after processing N tokens:

\(S_N = \sum_{i=1}^{N} \left(B_i \prod_{j=i+1}^{N} A_j\right)\)

Computational Advantages

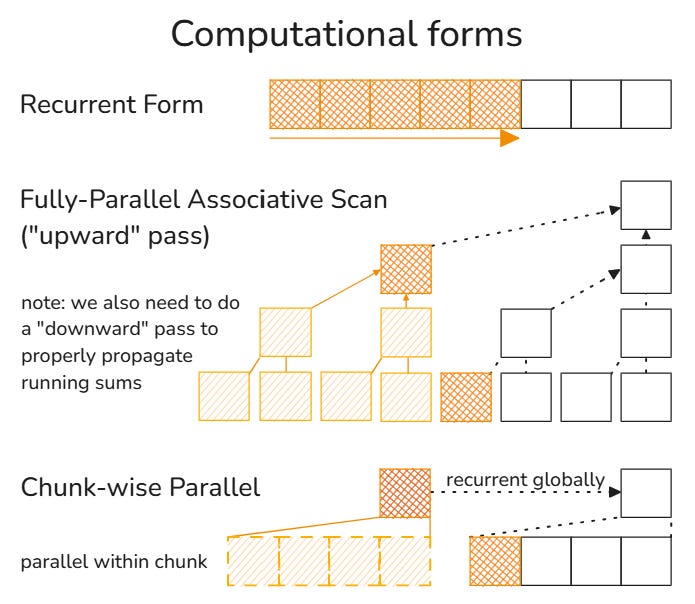
The blocked matrix formulation makes it evident why linear attention mechanisms can be parallelized at training time. Since updates are essentially blocked matrix multiplications, and matrix multiplications are associative, the associative scan algorithm can be employed to compute all intermediary states in $O(N)$ time[1]. This provides significant computational efficiency compared to traditional attention mechanisms.

Analysis of Specific Linear Attention Mechanisms

Vanilla Linear Attention

Formulation and Properties

Update Matrices:

\(A_i = I, B_i = v_i k_i^T\)

State Formula:

\(S_N = \sum_{i=1}^{N} v_i k_i^T\)

Advantages

• Simplest form of linear attention

• Computationally efficient

• Directly accumulates outer products of keys and values

Disadvantages

• Limited expressivity compared to other variants

• No forgetting mechanism to prioritize recent information

• May struggle with very long sequences as all information is given equal weight

Mamba 2

Formulation and Properties

Update Matrices:

\(A_i = \text{diag}\left(\alpha_i I\right), B_i = v_i k_i^T\)

State Formula:

\(S_N = \sum_{i=1}^{N} \left( \prod_{j=i+1}^{N} \alpha_j \right) v_i k_i^T\)

Advantages

• Incorporates a data-dependent weight decay mechanism via \alpha_i

• Controls how much of the previous state to keep or forget

• When \alpha_i \in [-1, 1], can learn more complex patterns while maintaining training stability

• Allows for selective forgetting of information based on context

Disadvantages

• More complex than vanilla linear attention

• Potential instability if \alpha_i values are not properly constrained

• May require more careful initialization and training procedures

DeltaNet

Formulation and Properties

Update Matrices:

\(A_i = I - \beta_i k_i k_i^T, B_i = \beta_i v_i k_i^T\)

State Formula:

\(S_N = \sum_{i=1}^{N} \left(\beta_i v_i k_i^T \prod_{j=i+1}^{N} \left(I - \beta_j k_j k_j^T\right)\right)\)

Advantages

• Features a data-dependent learning rate \beta_i that controls information addition

• When beta_i is in the range of the state update equation, allows for negative eigenvalues while maintaining norm bounds

• Can learn more complex patterns while ensuring training stability

• Provides a more nuanced approach to updating the state

Disadvantages

• More computationally intensive than vanilla linear attention

• Complex update rule may be harder to implement efficiently

• Requires careful tuning of the \beta_i parameter

Gated DeltaNet

Formulation and Properties

Update Matrices:

\(A_i = \alpha_i(I - \beta_i k_i k_i^T), B_i = \beta_i v_i k_i^T\)

State Formula:

\(S_N = \sum_{i=1}^{N} \left(\left(\beta_i \prod_{j=i+1}^{N} \alpha_j \right) v_i k_i^T \prod_{j=i+1}^{N} \left(I - \beta_j k_j k_j^T\right)\right) \)

Advantages

• Combines the benefits of both Mamba 2 and DeltaNet

• Features both data-dependent weight decay \alpha_i and learning rate \beta_i

• Offers more flexible control over state updates

• Can model complex dependencies in the sequence data

Disadvantages

• Most complex among the first four variants

• Potentially higher computational cost

• May be more challenging to implement and debug

• Requires tuning of multiple parameters

RWKV-7

Formulation and Properties

Update Matrices:

\(A_i = \text{diag}(w_i) - \hat{\kappa}_i(a_i \odot\hat{\kappa}_i^T), B_i = v_i k_i^T\)

State Formula:

\(S_N = \sum_{i=1}^{N} \left(v_i k_i^T \prod_{j=i+1}^{N} \left(\text{diag}(w_j) - \hat{\kappa}_j(a_j \odot\hat{\kappa}_j^T)\right)\right)\)

Advantages

• Provides a highly sophisticated update mechanism

• Likely the most expressive among the variants presented

• Can capture complex patterns in sequence data

• Builds on previous RWKV iterations with improved modeling capabilities

Disadvantages

• Most mathematically complex formulation

• Potentially highest computational cost

• May require more careful implementation and optimization

• Possibly more difficult to interpret and analyze

Multi-Step Online Gradient Descent per Token

Extending the Framework

The article extends the linear attention framework to support multiple gradient descent steps per token. Instead of taking just one update step per token, we can take n_h steps, following the approach outlined in the DeltaProduct paper:

1. Recurrently generate n_h key-value pairs for each input token

2. Update the state using these n_h key-value pairs

3. Keep only the final key-value pair and discard the rest

Mathematical Representation

In the blocked matrix formulation, this extension replaces each update with a product of n_h updates:

\(\begin{bmatrix} A_{i} & 0 \\ B_{i} & I \end{bmatrix} \longrightarrow \begin{bmatrix} A_{i,1} & 0 \\ B_{i,1} & I \end{bmatrix} \begin{bmatrix} A_{i,2} & 0 \\ B_{i,2} & I \end{bmatrix} \cdots \begin{bmatrix} A_{i,n_h} & 0 \\ B_{i,n_h} & I \end{bmatrix}\)

where A_{i,j} and B_{i,j} are the update matrices for the j-th gradient descent step for the i-th token.

Advantages and Implementation Options

The article presents two approaches to implementing this extension:

1. Direct computation using reindexed formula:

\(S_N = \sum_{k=1}^{Nn_h} \left( B_k \prod_{k'=k+1}^{Nn_h} A_{k'}\right) \)

2. First combining updates for each token before multiplying them together:

\( \begin{bmatrix} A'_{i} & 0 \\ B'_{i} & I \end{bmatrix} = \prod_{j=1}^{n_h} \begin{bmatrix} A_{i,j} & 0 \\ B_{i,j} & I \end{bmatrix} \)

Both approaches yield the same mathematical result but may differ in implementation efficiency.

Comparative Analysis

In terms of Expressivity vs. Complexity

The linear attention variants represent a spectrum of trade-offs between expressivity and complexity:

• Vanilla Linear Attention: Simplest but least expressive

• Mamba 2: Adds forgetting mechanism with minimal complexity increase

• DeltaNet: Implements data-dependent learning rate for more nuanced updates

• Gated DeltaNet: Combines forgetting and learning rate control for enhanced expressivity

• RWKV-7: Most complex formulation, likely with highest expressivity

Computational Efficiency vs. Modeling Power

While all these mechanisms maintain linear computational complexity with respect to sequence length (unlike quadratic complexity in traditional attention), they differ in their computational demands:

• Simpler mechanisms like Vanilla Linear Attention offer the fastest computation

• More complex variants like RWKV-7 require more computation but potentially capture more intricate patterns

• The multi-step gradient descent extension offers a way to increase modeling power at the cost of increased computation per token

HuggingFace has a really nice post on different other types of attention mechanisms focusing on their mathematical formulations, advantages, and limitations similar to above post, but might be more approachable for people who want to understand the intuition and less so about mathematical derivation and formulation(they do give the mathematical formulation in the post as well!)

1. Slim Attention

• Raison D’etre: Optimize memory usage and speed for processing long sequences.

• Core Idea: Instead of storing both keys (K) and values (V) in memory, Slim Attention reconstructs V from K using learned projections.

Implementation

• KV Cache Reduction:

Traditional attention stores separate K and V matrices. Slim Attention exploits their shared origin from input data, recalculating V dynamically from K using projection weights. This avoids storing redundant information.

• RoPE Handling:

Rotary Positional Embeddings (RoPE) are applied to K and queries (Q). To reconstruct V, Slim Attention either:

1. Stores raw K (without RoPE) and applies positional encoding during recomputation.

2. Reverses RoPE for sparsely accessed K vectors.

Advantages

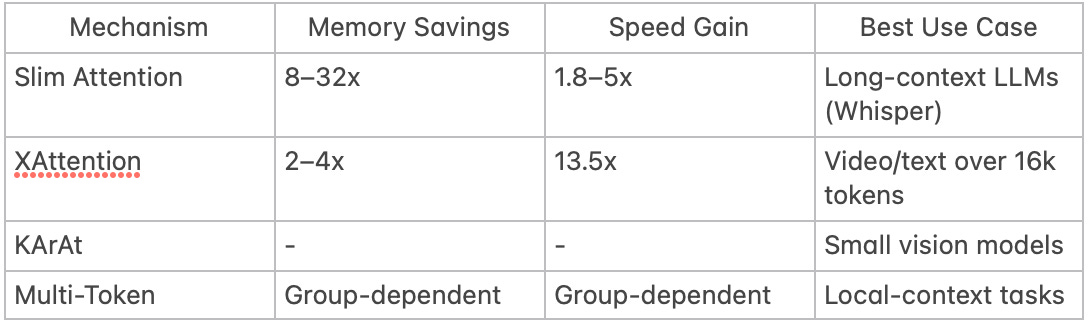
• Memory Efficiency: Reduces KV cache size by 50–90%, enabling 8–32x memory savings in models like Whisper and T5-11B.

• Speed: Achieves 1.8–5x faster inference, especially for large batches.

• Compatibility: Drop-in replacement for standard multi-head attention (MHA) in models like CodeLlama and Phi-3.

Limitations

• Compute Overhead: Rebuilding V adds ~15% computational cost.

• Incompatibility: Fails with multi-query (MQA) or grouped-query attention (GQA).

• Matrix Stability: Requires invertible projection matrices, challenging for non-square architectures.

2. XAttention

Raison D’etre: Accelerate block-sparse attention for long sequences (text, video).

Core Idea: Prioritizes critical blocks using antidiagonal sums for efficient pattern detection.

Implementation

• Antidiagonal Scoring:

Divides the attention matrix into blocks and scores them by summing values along diagonal lines. High-scoring blocks (indicative of vertical/diagonal patterns) are retained.

Dynamic Thresholding:

Adjusts sparsity per attention head using cumulative probability thresholds, balancing speed and accuracy.

Advantages

• Speed: 13.5x faster than dense attention on 16k-token sequences.

• Multimodal Support: Processes 1-hour videos (1 FPS) with 50% fewer computations.

• Accuracy: Matches full attention on LongBench (+2.1%) and RULER benchmarks.

Limitations

• Approximation Errors: May miss non-diagonal patterns.

• Warmup Phase: Requires 5 steps of full attention for stable video generation.

3. Kolmogorov-Arnold Attention (KArAt)

Raison D’etre: Replace static softmax with learnable, interpretable attention operators.

Core Idea: Uses spline-based activation functions inspired by Kolmogorov-Arnold Networks (KANs).

Implementation Details

• Basis Functions:

Decomposes attention scores into combinations of Fourier, B-spline, or wavelet functions. The model learns which basis functions to emphasize.

• Low-Rank Projection (Fourier-KArAt):

Compresses attention computations into a lower-dimensional space using Fourier features, reducing memory and compute costs.

Advantages

• Adaptability: Boosts accuracy by 5–7% on small vision models (ViT-Tiny).

• Interpretability: Produces sharper attention maps focused on salient image regions.

Limitations

• Scalability: Fails on larger models (ViT-Base) due to parameter explosion.

• Training Instability: Requires careful learning rate tuning.

4. Multi-Token Attention

Raison D’etre: Enable token groups to collaborate during attention computation.

Core Idea: Processes fixed-size token groups instead of individual tokens.

Implementation Details

• Grouped Attention:

Splits input into adjacent token groups (e.g., 3–5 tokens). Computes attention within each group, reducing sequence length and FLOPs.

Advantages

• Efficiency: Cuts computation by grouping factor squared (e.g., 9x for 3-token groups).

• Local Context: Captures idioms or phrases better than single-token attention.

Limitations

• Fixed Grouping: Struggles with long-range dependencies.

• Over-Smoothing: May dilute rare token importance.

Comparative Analysis

Dimension Comparisons

1. Memory vs. Compute Trade-offs:

• Slim Attention sacrifices compute for memory efficiency, ideal for deployment-scale models.

• XAttention balances both via intelligent sparsity, excelling in multimodal tasks.

2. Learnability vs. Stability:

• KArAt’s adaptive operators enhance small models but struggle with scalability.

• Multi-Token Attention simplifies computation but limits long-range reasoning.

3. Implementation Strategies:

• Slim and XAttention use block-wise optimizations for parallelization.

• KArAt requires low-rank approximations to remain practical.

Libraries

Dynamax is a library for probabilistic state space models (SSMs) written in JAX. It has code for inference (state estimation) and learning (parameter estimation) in a variety of SSMs, including:

• Hidden Markov Models (HMMs)

• Linear Gaussian State Space Models (aka Linear Dynamical Systems)

• Nonlinear Gaussian State Space Models

• Generalized Gaussian State Space Models (with non-Gaussian emission models)

The library consists of a set of core, functionally pure, low-level inference algorithms, as well as a set of model classes which provide a more user-friendly, object-oriented interface. It is compatible with other libraries in the JAX ecosystem, such as optax (used for estimating parameters using stochastic gradient descent), and Blackjax (used for computing the parameter posterior using Hamiltonian Monte Carlo (HMC) or sequential Monte Carlo (SMC)).

Edge is an open-source library to support the research and release of efficient state space models (SSMs) for on-device applications across multiple accelerators and environments.

Current state-of-the-art models are often too large and slow to run on-device, requiring cloud-based solutions that are expensive and slow. Edge aims to change this by providing a library of efficient SSM models that can run on-device in real-time.

State-Space Models (SSMs) offer a fundamentally more computationally efficient, yet high quality, approach to building AI models compared to Transformer models. They provide an elegant foundation for training efficient real-time models that can natively stream information with constant tokens per second (tok/s) and memory consumption, making them a game changer for on-device applications.

Introspect is a service that does data-focused deep research for structured data. It understands your structured data (databases or CSV/Excel files), unstructured data (PDFs), and can query the web to get additional context.

Benchmarks

Vector DB Comparison is a free and open source tool from Superlinked to compare vector databases. Each of the features outlined has been verified to varying degrees by the community.